Grid coordinates
We can think of a grid as a two-dimensional structure that can be accessed using
coordinates (row, column):

The cell that is colored blue has coordinates (1, 2), meaning it is in row 1,
column 2.
Using coordinates to access grid cells
Let’s write a print_grid() function that uses coordinates to access each cell:
def print_grid(grid):
for row in range(len(grid)):
for column in range(len(grid[row])):
print(grid[row][column], end='\t')
print()len(grid)= number of rows in the gridgrid[row]= a specific row of the grid, e.g.grid[1]= row 1len(grid[row])= number of columns in a specific row of the gridgrid[row][column]= item in the cell that is at location(row, grid)end='\t'= prints a tab character after the contents of each cell
If we call this function:
numbers = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
print_grid(numbers)then it will print:
1 2 3 4
5 6 7 8
9 10 11 12Traversing a grid by columns instead of rows
What happens if we change the order of the for loops in our print_grid()
function?
def print_grid_by_columns(grid):
for column in range(len(grid[0])):
for row in range(len(grid)):
print(grid[row][column], end='\t')
print()If we run this with the grid above, we get:
1 5 9
2 6 10
3 7 11
4 8 12The order of the loops controls the direction the grid is traversed.
Averaging the values of each row
Let’s write a function that computes the average of each row of a grid. It should return the averages in a list.
def row_average(grid):
result = []
for row in grid:
result.append(sum(row) / len(row))
return resultWe are using the built-in function
sum(), which can sum all the elements of a list.
If we run this function:
numbers = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
print(row_average(numbers))we get:
[2.5, 6.5, 10.5]Computing the maximum length of a string in a column
Working on columns is a little bit more challenging. Suppose we have a grid of strings:
fruits = [
['apple', 'pear', 'guava'],
['orange', 'banana', 'peach'],
['melon', 'mango', 'kiwi']
]Let’s write a function that computes the maximum length of the strings in each column, returning those maximums in a list.
def column_max_string_length(grid):
"""Returns the maximum length of the strings in each column. Assumes the grid is regular."""
maximums = []
for column in range(len(grid[0])):
max_length = None
for row in range(len(grid)):
item_length = len(grid[row][column])
if max_length is None or item_length > max_length:
max_length = item_length
maximums.append(max_length)
return maximumsWe have to loop through column to compute its maximum. To get the number of
columns we use len(grid[0]). As we look at a given column, we can loop through
all the rows and check the length of the item in that particular column.
If we run this code:
fruits = [
['apple', 'pear', 'guava'],
['orange', 'banana', 'peach'],
['melon', 'mango', 'kiwi']
]
print(column_max_string_length(fruits))the output is:
[6, 6, 5]Transposing a grid
Transposing a grid means flipping it diagonally:
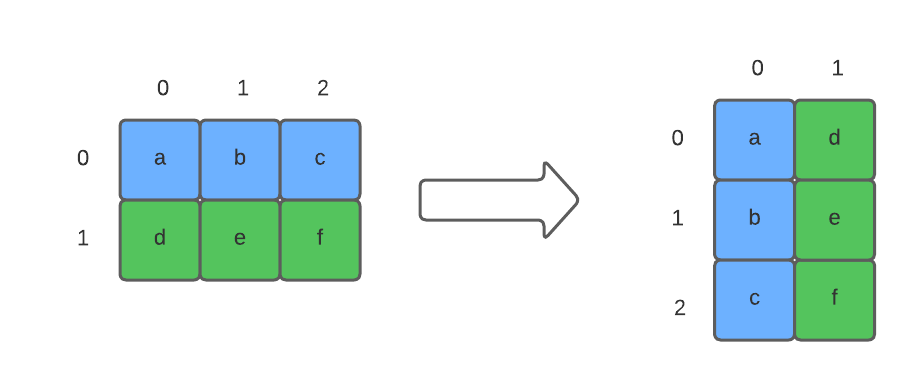
Notice how row 0 becomes column 0, and row 1 becomes column 1.
One way to do this is to copy each row into a column, and then append those columns into a new grid. Here is a solution that does that:
def transpose(grid):
"""Returns a tranposed copy of the grid."""
new_grid = []
# loop through all of the columns
for column in range(len(grid[0])):
# create a column
new_column = []
# loop through a row and append its values to a column
for row in range(len(grid)):
new_column.append(grid[row][column])
# append the column to the grid
new_grid.append(new_column)
return new_gridIf we run this:
my_grid = [
[1, 2],
[3, 4],
[5, 6],
[7, 8]
]
print_grid(my_grid)
print_grid(transpose(my_grid))the output is:
1 3 5 7
2 4 6 8An alternative transpose solution
A different way to think about this is to create a new grid that has the right
size we need, filled with None. This new grid needs its rows to be equal to
the number of columns in the original grid. Likewise, its columns should be
equal to the number of rows in the original grid. We can then copy the values
from each row into each column.
def make_empty_grid(rows, columns):
new_grid = []
for row in range(new_num_rows):
new_row = []
for column in range(new_num_columns):
new_row.append(None)
new_grid.append(new_row)
return new_grid
def transpose2(grid):
"""Returns a transposed copy of the grid."""
num_rows = len(grid)
num_columns = len(grid[0])
# make a new grid that is the right shape
new_grid = make_empty_grid(num_columns, num_rows)
# populate the new grid
for row in range(num_rows):
for column in range(num_columns):
new_grid[column][row] = grid[row][column]
return new_gridHelpful built-in functions
Python has some helpful built-in functions that you may find useful:
sum()- computes the sum of a list of numbersmax()- computes the maximum of a list of numbersmin()- computes the minimum of a list of numbers
Here are some examples:
numbers = [1, 2, 3, 4, 5]
sum(numbers)
min(numbers)
max(numbers)